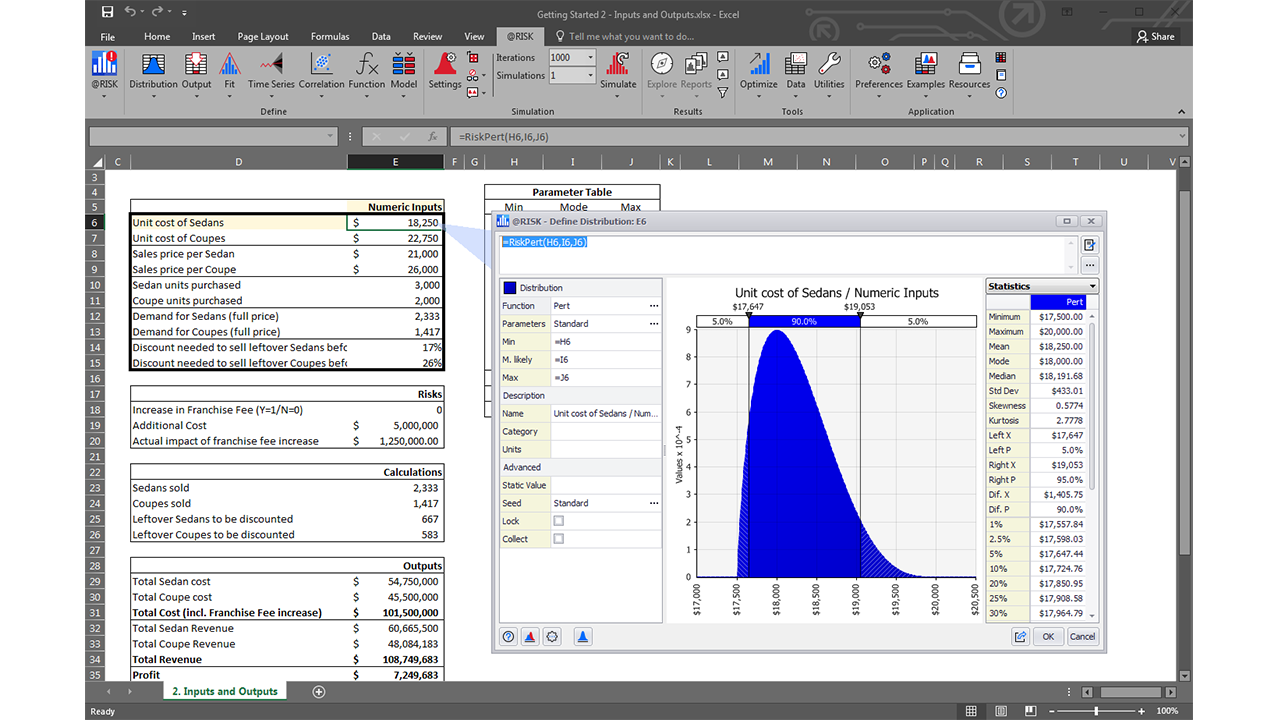
@RISK risk analyis software gives you multiple options for saving Monte Carlo simulations you have run and comparing them with other simulations. These include: Storing simulations in your Excel workbook Saving simulations as a separate.RSK5 file outside the workbook Using the @RISK Library for storing and comparing different simulations. @RISK Getting Started Guide Welcome to @RISK, the world’s leading Excel-based Monte Carlo simulation package! This short guide is designed to get you started using @RISK quickly. It is appropriate if you are either completely new to risk analysis using Monte Carlo simulation, or if you know those concepts well but are new to @RISK. The Palisade Risk Conference 2016 is being held on November 1 & 2, 2016. I have used Palisade’s DecisionTools Suite since my first year in graduate school (in the MSPM program at George Washington University) back in 2010. I love the power and utility of @Risk, the Excel add-in program for doing Monte Carlo simulations.
We can apply a risk matrix to a set of data to determine the risk that a hazard poses. We can do this with the INDEX and MATCH function. In this Matrix, the Y-axis tells us the SEVERITY of the risk involved and the X-axis tells us the LIKELIHOOD of occurrence of the RISK. Hence, the RISK of a hazard is calculated as:
Riskof hazard = likelihood of occurrence (probability) * Severity of harm
We will walk through the steps below to understand the process.
Figure 1: How to Use a Risk Matrix
Formula
The formula in Cell D13 is given as:
=INDEX(C5:G9,MATCH(Severity,B5:B9,0),MATCH(Likelihood,C4:G4,0))
Setting up the Data
We will set up the risk matrix by doing the following:
- We will type the severity on the Y-axis (Cell B5 to Cell B9)
- We will type the likelihood on the X-axis (Cell C4 to Cell G4)
- We will input the numbers as shown in figure 2 in the range of C5:G9
- Cell C11, C12, and C13 will be named likelihood, severity, and result respectively
- Cell D11 and D12 will be named as RARE and MODERATE respectively
Figure 2: Setting up the Risk Matrix Data
Determining the Risk
- We will click on Cell E11
- We will type in this string:
=MATCH(D11,C4:G4,0) - Click on Enter
- Likewise, we will click on Cell E12
- We will type in this string:
=MATCH(D12,B5:B9,0) - We will click on Enter
Figure 3: Determining the Result of the Inputted Data in the Risk Matrix
We will type the formula below into Cell D13
=INDEX(C5:G9,MATCH(D12,B5:B9,0),MATCH(D11,C4:G4,0))
Risk Excel Template
Figure 4: Determining the Result of the Inputted Data in the Risk Matrix
Risk Excel Plugin
We will press enter
Figure 5: Result of the Inputted Data in the Risk Matrix
Explanation
- MATCH function
The match function matches the lookup value within a specified range and we have set it to return an exact match. For instance, when determining the likelihood in the example, we typed in the string below:
=MATCH(D11,C4:G4,0)
D11 is the lookup value, C4:G4 is the range and zero indicates an exact match.
The same scenario applies to determine the severity.
- INDEX function
The INDEX function returns the number or value that is present in ROW 3 and COLUMN 2 based on this string: =INDEX(C5:G9,E11,E12)
This method is preferred to the ALTERNATIVE METHOD because we can vary the SEVERITY and LIKELIHOOD in Cells D11 and D12 respectively to AUTOMATICALLY get the result.
Alternative method
- We will click on Cell D13
- We will type the string below into the Cell
=INDEX(C5:G9,MATCH(D12,B5:B9,0),MATCH(D11,C4:G4,0)) - We will click on Enter
Figure 6: Result of the Alternative method of applying the Risk Matrix
Instant Connection to an Expert through our Excelchat Service
Most of the time, the problem you will need to solve will be more complex than a simple application of a formula or function. If you want to save hours of research and frustration, try our live Excelchat service! Our Excel Experts are available 24/7 to answer any Excel question you may have. We guarantee a connection within 30 seconds and a customized solution within 20 minutes.
Home → Techniques and Tips → Correlation in @RISK → How @RISK Correlates Inputs
Applies to: @RISK, all releases
How do I specify correlations?
When two or more input variables should be correlated, you can click the Define Correlations icon in the ribbon, specify correlations in the Model Definition Window, or add RiskCorrmat( ) functions directly to the distribution formulas for those variables in your Excel sheet.
The correlation coefficients you specify are Spearman rank-order correlations, not Pearson linear correlations. The rank-order correlation coefficient was developed by C. Spearman in the early 1900's, and this article explains how @RISK computes the rank-order correlation coefficient.
Pearson correlations assume linear distributions, but the great majority of distributions are non-linear, and Spearman is usually more appropriate for non-linear distributions. A Web search for choose Spearman or Pearson correlation will show lots of articles about the different uses of these two forms of correlation.
During a simulation, how does @RISK draw random numbers to achieve my specified correlations?
@RISK draws all samples for correlated variables before the first iteration of the simulation. (Non-correlated variables are sampled within each iteration.) Knowing the number of iterations to be performed, @RISK adjusts the ranking and associating of samples within each iteration to yield the defined correlation values. Again, this correlation is based on rankings of values, not actual values themselves as with the linear correlation coefficient. A value's 'rank' is determined by its position within the min-max range of possible values for the variable.
@RISK generates rank-correlated pairs of sampled values in a two-step process:
A set of randomly distributed 'rank scores' is generated for each variable. If 100 iterations are to be run, for example, 100 scores are generated for each variable. (Rank scores are simply values of varying magnitude between a minimum and maximum. @RISK uses van der Waerden scores based on the inverse function of the normal distribution.) These rank scores are then rearranged to give pairs of scores which generate the desired rank-order correlation coefficient. For each iteration there is a pair of scores, with one score for each variable.
A set of random numbers (between 0 and 1) to be used in sampling is generated for each variable. Again, if 100 iterations are to be run, 100 random numbers are generated for each variable. These random numbers are then ranked smallest to largest. For each variable, the smallest random number is then used in the iteration with the smallest rank score, the second smallest random number is used in the iteration with the second smallest rank score, and so on. This ordering based on ranking continues for all random numbers, up to the point where the largest random number is used in the iteration with the largest rank score
This process results in a set of paired random numbers that can be used in sampling values from the correlated distributions during an iteration of the simulation.
This method of correlation is known as a 'distribution-free' approach because any distribution types may be correlated. Although the samples drawn for the two distributions are correlated, the integrity of the original distributions is maintained. The resulting samples for each distribution reflect the distribution function from which they were drawn.
Does @RISK use Cholesky decomposition?
Risk Excellence Definition
Yes. If Cholesky fails, the matrix is not self-consistent, and @RISK proceeds as in How @RISK Adjusts an Invalid Correlation Matrix.
If Cholesky succeeds, @RISK proceeds as in Iman, R. L., and W. J. Conover. 1982. 'A Distribution-Free Approach to Inducing Rank Correlation Among Input Variables.' Commun. Statist.-Simula. Computa. 11: 311-334. Retrieved 2018-08-23 from https://www.uio.no/studier/emner/matnat/math/STK4400/v05/undervisningsmateriale/A distribution-free approach to rank correlation.pdf.
Why does Excel report a different correlation from the one I specified?
This correlation method yields a rank order correlation (Spearman coefficient) that is usually quite close (within normal statistical variability) to your specified value. However, Excel's =CORREL( ) function reports the Pearson coefficient. The Pearson value may vary somewhat from the Spearman value, depending on the exact nature of the correlated distributions. This difference is illustrated in the attached workbook. (Beginning with @RISK 5.5, you can use the =RiskCorrel( ) worksheet function to display the Spearman or Pearson correlation for simulated data.)
Correlation of discrete distributions can be a particular problem. For more on that, please see Correlation of Discrete Distributions.
See also:Correlation in @RISK collects over a dozen articles explaining various aspects.
Risk Excel Templates
Additional keywords: Corrmat property function

Last edited: 2018-08-23